Note: JavaSketchpad cannot
support this GSP file. To move the points P, you must
open the GSP file IT4EMLociFixedAngle.gsp (see
above).
| Question 5: | Infer by induction
the locus of P such that angle APB is always 40o.
|
LOCI IT LESSON 2 - OTHER TYPES OF LOCI
(SEC 4 ELEMENTARY MATHEMATICS)
Software: JavaSketchpad (JSP)
Thinking Skills: Induction and
Deduction
At the end of the lesson, the students should be able to:
(1) describe the loci of a few interesting examples,
(2) construct the above loci.
It takes a few seconds to initialise the JavaSketch below. But if the
toolbar at the bottom reads, "Applet not found", click
here to troubleshoot.
| The first JavaSketch (IT4EMLociCoin.gsp) shows
a coin, centre O and radius 1 cm, inside a circular ring of radius 4 cm.
If the coin moves such that it is always in contact with the ring, what
is the locus of the centre O of the coin?
Drag the point of contact C and see the various positions that O can
move to. Alternatively, click on the button "Animate".
|
B.
LOCUS OF MIDPOINT OF LADDER
| The second JavaSketch (IT4EMLociLadder.gsp)
shows a ladder AB leaning against a wall. If the ladder slides down the
wall such that its foot is always in contact with the floor, what is the
locus of its midpoint M?
Drag the point B and see the various positions that M can move to. Alternatively,
click on the button "Animate".
|
C.
LOCUS OF TRIANGLE WITH SAME AREA
| The third JavaSketch (IT4EMLociTriangleArea.gsp)
shows a triangle ABC and two positions of a point P. PQ is the height of
triangle ABP. If the area of triangle ABP must be equal to the area of
triangle ABC, what is the locus of the point P?
Drag the point P and see the various positions that P can move to. Alternatively,
click on the buttons "Animate"
and "Animate".
|
| The fourth JavaSketch (IT4EMLociAngle90.gsp)
shows angle APB=90o. If P moves such that angle APB remains
90o, what is the locus of the point P?
Drag the point P and see the various positions that P can move to. Alternatively, click on the button "Animate". Note: JavaSketchpad cannot
support shading of the angle APB. To see this, open the GSP file IT4EMLociAngle90.gsp
using Geometer's
Sketchpad. If you have problems opening this file, click
here.
|
E.
LOCUS OF FIXED ANGLE NOT EQUAL TO 90o
JavaSketchpad cannot support this
sketch, so you have to open the GSP file (IT4EMLociFixedAngle.gsp)
using the Geometer's
Sketchpad software which has a free evaluation version. Click on
the hyperlink above and choose the option "Open it" instead of "Save it
to disk". If you are using GSP for the first time,
a dialogue box "Open With" will appear. If you don't know what to do, click
here.
 |
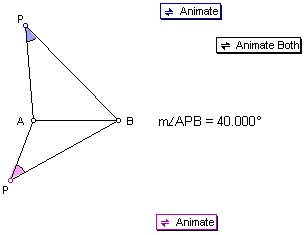
The fifth picture (IT4EMLociFixedAngle.gsp)
shows angle APB=40o with two positions of the point P. If P
moves such that angle APB remains 40o, what is the locus of
the point P?
Note: JavaSketchpad cannot
support this GSP file. To move the points P, you must
open the GSP file IT4EMLociFixedAngle.gsp (see
above).
|
F.
LOCUS OF MIDPOINT OF LINE JOINING TWO CIRCLES (ENRICHMENT)
| The sixth JavaSketch (IT4EMLociTwoCircles.gsp)
shows a line PQ joining two circles. If P and Q move round their respective
circles in the same direction, what is the locus of the midpoint M of the
line PQ?
You cannot drag the points P and Q at the same time. So click on the button "Animate" to see the various positions that M can move to. It is not easy to describe this locus in words. But do you see a pattern with some heart shapes? Click here for answer (it shows animation in a different way). |
G. WITCH
OF AGNESI (ENRICHMENT)
| Maria Agnesi (1719-1799) of Italy was a gifted
linguist and mathematician. She is famous for this curve known incorrectly
as the "Witch of Agnesi". Agnesi named this curve as "la versiera" which
means "rope that turns into a sail". But a translator mistook this word
as "l'aversiera" which means "witch".
The seventh JavaSketch (IT4EMLociWitch.gsp) shows a circle with its diameter on the y-axis and the origin O. The tangent to the circle parallel to the x-axis intersects the line joining O and A at a point which the vertical line through P must pass. If the point A moves round the circle such that AP is always parallel to the x-axis, where can P move? Drag the point A and see the various positions that P can move to. Alternatively, click on the button "Animate". Click here for answer (it shows animation in a different way). |
H. EXERCISE
Apply what you have learnt to deduce
the answers to this exercise. Please refer to the Maths Online IT Workbook
for the exercise.