| 1. |
How do you prove that the definite integral gives the area
under a curve? We use the Riemann Sums for very large n (or for very small  x,
i.e. as x,
i.e. as  x x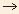 0).
This shows the link between the numerical methods and the calculus method. 0).
This shows the link between the numerical methods and the calculus method. |
| |
|
| 2. |
Consider the diagram in the Worksheet. P(x, y) and Q(x+ x,
y+ x,
y+ y) are 2 points
on the curve near to each other. y) are 2 points
on the curve near to each other. |
|
From Question 10, LowerSum < Area < UpperSum. Thus |
|
Area of Rectangle PSRU < Area Under Curve < Area of Rectangle
TSRQ
|
|
PS x SR <  A
< TS x SR A
< TS x SR
|
|
y x
< x
<  A <
(y+ A <
(y+ y) y) x x
|
|
y < 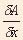 <
y+ <
y+ y y
|
|
As  x x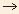 0, 0,  y y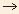 0. 0. |
|
So 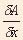 ,
which is bounded by lower limit y and upper limit y+ ,
which is bounded by lower limit y and upper limit y+ y y 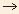 y, has to become y as
y, has to become y as  x x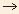 0. 0. |
|
Therefore 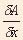 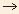 y as
y as  x x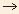 0,
i.e. 0,
i.e. 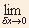 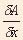 = y.
= y. |
|
But you have learnt in Differentiation IT Lesson 1 - Gradient Function
that 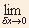 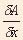 =
= 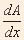 . . |
|
Therefore 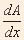 = y, i.e. if you differentiate the area A under
a curve, you get the equation y of the curve!
= y, i.e. if you differentiate the area A under
a curve, you get the equation y of the curve! |
| |
|
| 3. |
Recall that integration is the reverse of differentiation, i.e. 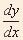 = y'
= y' 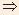 y =
y = 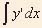 . . |
|
Therefore 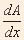 = y
= y 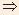 A =
A = 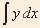 . . |
|
Recall the definition of the definite integrals which say that 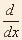 [F(x)]
= f(x) [F(x)]
= f(x) 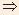 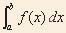 = F(b) – F(a).
= F(b) – F(a). |
|
Now area under a curve from x = a to x = b is given by A(b) – A(a)
where we treat A as a function. |
|
Therefore area under a curve from x = a to x = b is A(b) – A(a) = 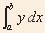 , , |
|
i.e. if you integrate the equation y of a
curve from x = a to x = b, you get the area under the curve! |
| |
|
| |
|
| 4. |
From Sect E para 5, the Riemann Sum 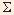 (y (y x) x)  A as
A as  x x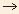 0. 0. |
|
Since A = 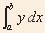 ,
then ,
then 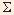 (y (y x) x) 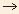 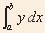 as
as  x x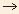 0, 0, |
|
i.e. the Riemann Sum 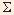 (y (y x)
becomes the definite integral x)
becomes the definite integral 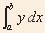 as
as  x x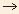 0
(or as n becomes bigger). 0
(or as n becomes bigger). |
|
This is the link between the numerical methods and the calculus method.
The integral, as defined in this way, is called the Riemann
integral. For info, there are integrals defined in other ways. |
| |
|
| 5. |
It is important to note that the definite integral is a limit,
just like the derivative (or the gradient function). |
| |
|
| |
|
| 6. |
Now that we have learnt the calculus method, what is the use of the
numerical methods?
| (a) |
Many expressions cannot be integrated, e.g. sin x2.
So you still need the numerical methods to approximate the definite integral. |
| (b) |
It will take a long time to integrate complicated expressions (which
can be integrated). In such cases, LiveMath will ask you whether to proceed
with the integration or to use a numerical method which is still faster. |
| (c) |
LiveMath is a computer algebra system (CAS), unlike most other software.
It can perform algebraic operations like factorisation, differentiation
and integration. Non-CAS will use a numerical method to find the answers. |
|