Rotation

TRANSFORMATION IT LESSON 2 - ROTATION
(SEC 4 ELEMENTARY MATHEMATICS)

Software: JavaSketchpad (JSP) – need Geometer's Sketchpad (GSP)
Thinking Skills: Induction and Deduction
At the end of the lesson, the students should be able to:
(1) infer by induction the property of the image under a rotation,
(2) construct the image under a rotation about any centre,
(3) derive formulae for the coordinates of the image under rotations of 90^o, 180^o and 270^o anticlockwise about the origin,
(4) find the invariant point under a rotation,
(5) find the centre of rotation given an object and its image.

A. PROPERTY OF IMAGE UNDER ROTATION

It takes a few seconds to initialise the JavaSketch below. But if the toolbar at the bottom reads, "Applet not found", click here to troubleshoot.

Sorry, this page requires a Java-compatible web browser.

1. The first JavaSketch (IT4EMTransfRotation1.gsp) shows a triangle ABC and its image A'B'C' under a rotation of 90^o anticlockwise about the centre O. Observe the shapes and sizes of the object and the image.

2. Move the points A, B and C anywhere. Try making the object ABC an equilateral triangle, an isosceles triangle, a scalene triangle and a right-angled triangle. Observe the shapes and sizes of the object and the image.

3. You can also move the centre of rotation anywhere. Once again, observe the shapes and sizes of the object and the image.

Question 1: Infer by induction the shape and size of the image under a rotation.

Such a transformation that preserves the shape and size of the object is called an __________ transformation.

Question 2: What do you observe about angle AOA', the angle between the line joining the object A to the centre O and the line joining the centre O to the image A'?
Angle AOA' = ____^o = Angle of ____________.

This property will help you to construct the image of an object under a rotation.

B. ROTATION OF 90 DEGREES ANTICLOCKWISE

JavaSketchpad cannot support grid lines, so you have to open the GSP file (IT4EMTransfRotation2.gsp) using the Geometer's Sketchpad software which has a free evaluation version. Click on the hyperlink above and choose the option "Open it" instead of "Save it to disk". If you are using GSP for the first time, a dialogue box "Open With" will appear. If you don't know what to do, click here. The diagram below is just a non-interactive picture of the sketch.

1. The second sketch (IT4EMTransfRotation2.gsp) shows a triangle ABC with the origin O as the centre of rotation. The coordinates of the vertices are A(–3,4), B(–4,2) and C(–1,1). The angle of rotation is set as 90^o anticlockwise. Using the property in Question 2, write down the vertices of the image in the table in the Worksheet.

2. Double-click the button "Show Image" to check your answers.

3. Double-click the button "Hide Image". Then move the vertices of the triangle to A(1,3), B(–3,1) and C(–1,–2). Write down the vertices of the image in the table in the Worksheet.

4. Double-click the button "Show Image" to check your answers.

Question 3: By observing the coordinates of the 6 points and their images, derive a formula for the coordinates of an image under a rotation of 90^o anticlockwise about the origin O.
The point P(x, y) is mapped onto the image P'(___ , ___).

C. ROTATION OF 90 DEGREES CLOCKWISE

JavaSketchpad cannot support grid linesm, so you have to open the GSP file (IT4EMTransfRotation3.gsp) using the Geometer's Sketchpad software which has a free evaluation version. Click on the hyperlink above and choose the option "Open it" instead of "Save it to disk".

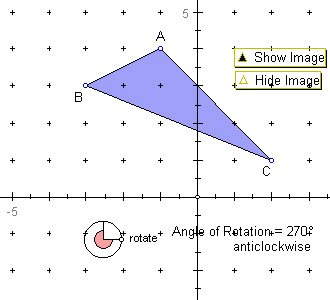
1. The third sketch (IT4EMTransfRotation3.gsp) shows a triangle ABC with the origin O as the centre of rotation. The coordinates of the vertices are A(–1,4), B(–3,3) and C(2,1). The angle of rotation is set as 270^o anticlockwise or 90^o clockwise. Write down the vertices of the image in the table in the Worksheet.

2. Double-click the button "Show Image" to check your answers.

3. Double-click the button "Hide Image". Then move the vertices of the triangle to A(1,3), B(–3,–2) and C(0,0). Write down the vertices of the image in the table in the Worksheet.

4. Double-click the button "Show Image" to check your answers.

Question 4: By observing the coordinates of the 6 points and their images, derive a formula for the coordinates of an image under a rotation of 90^o clockwise about the origin O.
The point P(x, y) is mapped onto the image P'(___ , ___).

Question 5: What do you notice about the image of the point C(0,0) in the second triangle in Paragraph 3 above?

Such a point is called an _____________ point. It will always lie on the ________ of _____________ .

D. ROTATION OF 180 DEGREES (HALF-TURN)

JavaSketchpad cannot support grid lines, so you have to open the GSP file (IT4EMTransfRotation4.gsp) using the Geometer's Sketchpad software which has a free evaluation version. Click on the hyperlink above and choose the option "Open it" instead of "Save it to disk".

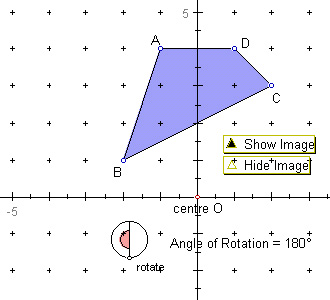
1. The fourth sketch (IT4EMTransfRotation4.gsp) shows a quadrilateral ABCD with the origin O as the centre of rotation. The coordinates of the vertices are A(–1,4), B(–2,1), C(2,3) and D(1,4). The angle of rotation is set as 180^o. Write down the vertices of the image in the table in the Worksheet.

2. Double-click the button "Show Image" to check your answers.

3. Double-click the button "Hide Image". Then move the vertices of the quadrilateral to A(–1,3), B(–2,2), C(0,0) and D(2,2). Write down the vertices of the image in the table in the Worksheet.

4. Double-click the button "Show Image" to check your answers.

Question 6: By observing the coordinates of the 8 points and their images, derive a formula for the coordinates of an image under a rotation of 180^o about the origin O.
The point P(x, y) is mapped onto the image P'(___ , ___).

Question 7: Which vertex of the second quadrilateral is invariant?

E. ROTATION ABOUT CENTRE OTHER THAN THE ORIGIN

JavaSketchpad cannot support grid lines, so you have to open the GSP file (IT4EMTransfRotation5.gsp) using the Geometer's Sketchpad software which has a free evaluation version. Click on the hyperlink above and choose the option "Open it" instead of "Save it to disk".

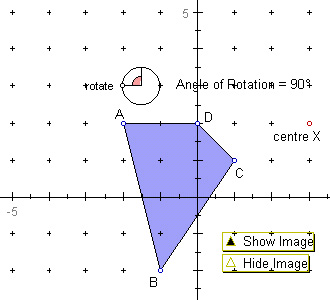
1. The fifth sketch (IT4EMTransfRotation5.gsp) shows a quadrilateral ABCD with the point X(3,2) as the centre of rotation. The coordinates of the vertices are A(–2,2), B(–1,–2), C(1,1) and D(0,2). The angle of rotation is set as 90^o anticlockwise. Write down the vertices of the image in the table in the Worksheet.

2. Double-click the button "Show Image" to check your answers.

3. Change the angle of rotation by moving the point "rotate" at the top left hand corner. Observe how the image moves for different angles of rotation.

Question 8: By observing the coordinates of the 4 points and their images, do you notice any pattern that will enable you to derive a formula for the coordinates of an image under a rotation of 90^o about the point X(3,2)?

F. HOW TO FIND CENTRE OF ROTATION

JavaSketchpad cannot support grid lines, so you have to open the GSP file (IT4EMTransfRotation6.gsp) using the Geometer's Sketchpad software which has a free evaluation version. Click on the hyperlink above and choose the option "Open it" instead of "Save it to disk".

If you are using GSP Version 4, open this file: IT4EMTransfRotation6_v4.gsp.

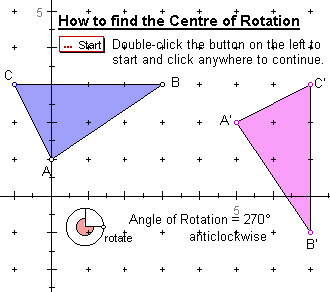
1. The sixth sketch (IT4EMTransfRotation6.gsp) shows a triangle ABC and its image A'B'C' under a rotation of 90^o clockwise. The coordinates of the vertices of the object and the image are A(0,1), B(3,3), C(–1,3), A'(5,2), B'(7,–1) and C'(7,3) respectively.

2. Double-click the button "Start" to show how to find the centre of rotation. It will stop at each step. Click anywhere to continue.

Question 9: State the coordinates of the centre of rotation.

Question 10: Move the vertices of triangle ABC anywhere. The image will move accordingly. Change the angle of rotation to 90^o anticlockwise. Double-click the button "Start" to find the centre of rotation. State its coordinates.

Question 11: Summarise the 5 steps needed to find the centre of rotation.
Step 1: __________________________________________
Step 2: __________________________________________
Step 3: __________________________________________
Step 4: __________________________________________
Step 5: __________________________________________

Question 12: Change the angle of rotation to 180^o. Double-click the button "Start" to find the centre of rotation. What do you notice about the point of intersection of the lines AA' and BB'?

Question 13: If the angle of rotation to 180^o, how do you simplify the method in Question 11 to find the centre of rotation?
Step 1: __________________________________________
Step 2: __________________________________________
Step 3: __________________________________________

Question 14: If there is an invariant point under a rotation, how do you find the centre of rotation?

Note: There are 3 ways to find the centre of rotation, depending on the angle of rotation and the image:

(i) If there is an invariant point, see Question 14.

(ii) If angle of rotation = 180^o, see Question 13.

(iii) For the general method, see Question 11.

[Return to top]

IT Menu | GSP | LiveMath


Question 1:	Infer by induction the shape and size of the image under a rotation.
	Such a transformation that preserves the shape and size of the object is called an __________ transformation.


Question 2:	What do you observe about angle AOA', the angle between the line joining the object A to the centre O and the line joining the centre O to the image A'? Angle AOA' = ____^o = Angle of ____________.
	This property will help you to construct the image of an object under a rotation.


Question 3:	By observing the coordinates of the 6 points and their images, derive a formula for the coordinates of an image under a rotation of 90^o anticlockwise about the origin O. The point P(x, y) is mapped onto the image P'(___ , ___).


Question 4:	By observing the coordinates of the 6 points and their images, derive a formula for the coordinates of an image under a rotation of 90^o clockwise about the origin O. The point P(x, y) is mapped onto the image P'(___ , ___).

Question 5:	What do you notice about the image of the point C(0,0) in the second triangle in Paragraph 3 above?
	Such a point is called an _____________ point. It will always lie on the ________ of _____________ .


Question 6:	By observing the coordinates of the 8 points and their images, derive a formula for the coordinates of an image under a rotation of 180^o about the origin O. The point P(x, y) is mapped onto the image P'(___ , ___).

Question 7:	Which vertex of the second quadrilateral is invariant?


Question 8:	By observing the coordinates of the 4 points and their images, do you notice any pattern that will enable you to derive a formula for the coordinates of an image under a rotation of 90^o about the point X(3,2)?


Question 9:	State the coordinates of the centre of rotation.

Question 10:	Move the vertices of triangle ABC anywhere. The image will move accordingly. Change the angle of rotation to 90^o anticlockwise. Double-click the button "Start" to find the centre of rotation. State its coordinates.

Question 11:	Summarise the 5 steps needed to find the centre of rotation. Step 1: __________________________________________ Step 2: __________________________________________ Step 3: __________________________________________ Step 4: __________________________________________ Step 5: __________________________________________

Question 12:	Change the angle of rotation to 180^o. Double-click the button "Start" to find the centre of rotation. What do you notice about the point of intersection of the lines AA' and BB'?

Question 13:	If the angle of rotation to 180^o, how do you simplify the method in Question 11 to find the centre of rotation? Step 1: __________________________________________ Step 2: __________________________________________ Step 3: __________________________________________

Question 14:	If there is an invariant point under a rotation, how do you find the centre of rotation?