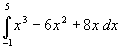Graphmatica

INTRODUCTION

Graphmatica is a friendly equation plotter written by Keith Hertzer, kSoft, Inc.. The program may be downloaded at kSoft's website at http://www8.pair.com/ksoft/ or here.

This document is an attempt to provide an introduction to the use of Graphmatica. You should try and read this with the software handy to try out the exercises.

The best way to learn the basics of Graphmatica is to explore it. When you first run the software, you will see a window similar to the one shown below:

A typical Graphmatica start up screen

The Menu Bar and Tool Bar are similar to most Windows programs. You key in your functions or equations to be plotted in the Equation Entry Bar and the graph will appear on the Graph Paper.

THE BASICS

Try the following exercises with Graphmatica. Menu items are indicated in CAPITAL LETTERS and menu options in italics.

1. Select File, Open List. Select the following demonstration graphs. Click on the different coloured graphs, taking note of the description of the graphs.
   1. xydemo.gr
   2. trig.gr
   3. inequal.gr
   4. polar.gr
   
   
   

   Note : the CLEAR button and REDRAW menu.

2. To plot graphs, all we need to do is to type the equations in the Equation Entry Bar. Plot the following graphs :
   

   Note: we need to type " x^2 " to denote the square of x.

   Click on the scroll arrow (to the right of the equations) to view the above equations.

   You can give this set of graphs a title (Select Labels, Title) and save the file (Select File, Save As).
   
   

3. Key in the equation y + x = 2y - x . Take note of the error message.
   
   
4. Select View, Graph paper, Trigonometric. Plot the following graphs.
   1. 
   2. 
   3. 

Note : y = sin x {0,2p} sketches the graph of for x between 0 and 2p.

INTERMEDIATE

1. Plot the graphs of the following inverse trigonometric functions (see Section 4.2 of Quick Reference)
   1. and
   2. and
   3. and

   What do you notice about the graphs of the inverse functions ?

2. Plot the following polar graphs on polar graph paper (Select View, Graph paper, Polar): . Describe these graphs, taking note of any special features.

3. A graph has polar equation , where a is a constant. Sketch the graph in the case . Try other values of a. Describe the graphs.

4. Plot the curve whose equation in polar coordinates is . Use the "Zoom In" feature to describe the shape of the curve near the pole.
5. Plot the following graphs of the following functions defined parametrically.
   1. 
   2. 
   3. 

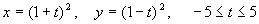
   (Example: x=(cos t)^3;y=(sin t)^3 {-p,p} sketches (a). Note the semicolon separating the x-function and the y-function)

6. Plot the following families of functions.
   1. 
   2. 
   3. 
   4. 
   5. 

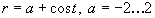
   (Example: y=a*x+2 {a:-5,5,1} sketches (a). The braces indicate that the variable a increases from -5 to 5 in steps of 1)

ADVANCED

1. Find the region satisfied by the simultaneous equations and . Determine the vertices of the region. (Select "Coord Cursor" Button. Point to an intersection point, click and read off the coordinates at the bottom of the screen).
2. Draw the graph of .
   1. draw the tangent to the curve at the point (1,3) and read off the gradient of the curve at this point (Select Calculus, Draw Tangent and click at the point (1,3)).
   2. Estimate
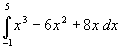   . (Select Calculus, Integrate. Position the cursor at the point (-1,-15). Drag the cursor along the x-axis to the point (5,0). Read off the answer at the bottom of the screen).
3. Draw the following graphs and state the relationship between the graphs:
   1. 
   2. 
   3. 
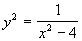
4. Let . The series expansion of up to the term in is . By plotting the graphs of and by taking successive terms of the series expansion, show that the series expansion gives a good approximation to . Determine the interval of x for which the approximation is particularly good.
5. Sketch the slope field of the differential equation . Obtain the graph for the particular case where
   1. 
   2. 
   3. 

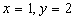
   (Enter dy+3*y=x in the equation bar to get slope field. To get the particular solution, enter dy+3*y=x {x-value,y-value}).

6. Given the differential equation where . Graph the function for